Grundlagen der Kondensatoren-Technologie
Grundprinz: Der Plattenkondensator
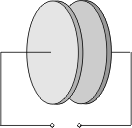
Zwei gleich große Metallplatten stehen sich in gewissem Abstand, durch Luft oder einen anderen Isolator getrennt, gegenüber. Eine Spannung wird angelegt:
Der Kondensator nimmt auf der Oberfläche seiner Platten einerseits negative und andererseits positive Ladungsträger auf. Er speichert sozusagen elektrische Ladung
(Mech. Analogon: Gefäß als "Speicher" für Flüssigkeit).
Gleichstrom läßt dieses Gebilde normalerweise nicht durch, die Elektronen können infolge des dazwischenliegenden Isolators (Dielektrikum) nicht von der einen Platte zur anderen gelangen. Nur bei sehr hohen Spannungen ist dies möglich, dann erfolgt ein "Durchschlag" durch Ionisation.
Merke: Für Gleichstrom ist der Kondensator normalerweise ein unendlich großer Widerstand.
Wechselstrom läßt der Kondensator dagegen durch. Zwar kann der Strom auch hier nicht direkt durch das Dielektrikum fließen, jedoch entsteht durch das wechselseitige Auf- und Entladen der Platte die Fiktion als würden Ladungsträger durch den Kondensator hindurchtransportiert werden. Natürlich stellt der Kondensator auch für Wechselstrom einen gewissen Widerstand dar, dieser ist abhängig von der Frequenz.
Merke: Bei niederen Frequenzen ist der kapazitive Widerstand größer, bei höheren Frequenzen ist er geringer.
Dielektrikum
In der Realität ist das Dielektrikum kein idealer Isolator, d. h. eine gewisse Anzahl von Elektronen durchdringt es.
Durch diese Vorgänge, sowie durch Umpolarisationen im Material geht ein Teil der elektrischen Energie als Verlustwärme verloren:
a) Ohmische Verluste: Man unterscheidet zwischen dem Isolationswiderstand = innerer Widerstand Ri (Stromdurchfluß durch das Innere des Isolators) und dem Oberflächenwiderstand = äußerer Widerstand Ra (Stromfluß über die Oberfläche des Isolators infolge Feuchtigkeit oder Verschmutzung). Beide zusammen ergeben den Gesamtwiderstand.
Die Ohmschen Verluste drücken sich in einer oft nicht unbeträchtlichen Erwärmung des Isolators aus.
b) Dielektrische Verluste entstehen infolge der durch Wechselfelder bedingten Umpolarisation der Elementarteilchen des Dielektrikums. Sie werden in Schwingungen versetzt (wie kleine Kompassnadeln) und erzeugen dabei Reibungswärme. Auch hier geht ein Teil der elektrischen Energie als Wärme verloren.
Die Verluste betragen:
tanδ heißt Verlustfaktor, er ist ein Maß für dielektrische Verluste und ist frequenzabhängig.
a) Ohmische Verluste: Man unterscheidet zwischen dem Isolationswiderstand = innerer Widerstand Ri (Stromdurchfluß durch das Innere des Isolators) und dem Oberflächenwiderstand = äußerer Widerstand Ra (Stromfluß über die Oberfläche des Isolators infolge Feuchtigkeit oder Verschmutzung). Beide zusammen ergeben den Gesamtwiderstand.
| Rges = Ri · RaRi + Ra |
Die Ohmschen Verluste drücken sich in einer oft nicht unbeträchtlichen Erwärmung des Isolators aus.
b) Dielektrische Verluste entstehen infolge der durch Wechselfelder bedingten Umpolarisation der Elementarteilchen des Dielektrikums. Sie werden in Schwingungen versetzt (wie kleine Kompassnadeln) und erzeugen dabei Reibungswärme. Auch hier geht ein Teil der elektrischen Energie als Wärme verloren.
Die Verluste betragen:
| P = Ueff2 · 2 · π · f · C · tanδ |
tanδ heißt Verlustfaktor, er ist ein Maß für dielektrische Verluste und ist frequenzabhängig.
Nennkapazität
| Definition: | Maßgröße für einen Kondensator ist seine Kapazität. Kapazität ist das elektrische Fassungsvermögen eines Kondensators, d. h. welche Menge an elektrischen Ladungsträgern (Elektronen) er aufnehmen kann. | |||||
| Bezeichnung: | C | |||||
| Maßeinheit: | F = Farad |
|||||
| Berechnungsbeispiel: |
Die Kapazität beträgt 1 Farad wenn bei einer angelegten Spannung von 1 V eine Sekunde lang ein Strom von 1 Ampere fließt |
|||||
Q ~ U
Der Proportionalitätsfaktor C ist die Kapazität eines Kondensators
Q = C · U
Kapazitätsberechnung des Plattenkondensators
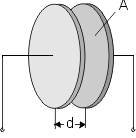
| C = ɛ0 · ɛr · Ad |
| ɛ0 |
= absolute Dielektrizitätskonstante = 0,0885 · 10-12 Farad/cm |
| ɛr . | = relative Dielektrizitätskonstante, abhängig vom Isoliermaterial |
| A | = Plattenfläche (nur einer Platte) in cm2 |
| d | = Plattenabstand in cm |
Die relative Dielektrizitätskonstante kann Werte zwischen ɛr = 1 (Luft) und ɛr ~ 10 000 (spezielle Keramikmassen) haben.
Kapazitätstoleranz
Toleranz ist die zulässige relative, in Prozent ausgedrückte Abweichung des Kapazitätswertes vom Nennwert. Die Toleranz muß bei +20°C gemessen werden und gilt nur für den Zeitpunkt der Auslieferung.
Nach längerer Lagerung oder längerem Gebrauch kann die Toleranz nach oben abweichen; jedoch darf sie nach Norm niemals den doppelten Wert der Auslieferung überschreiten.
Üblich sind bei Wickelkondensatoren folgende Auslieferungstoleranzen:
±1%; ±2,5%; ±5%; ±10%; ±20%.
Bei Elektrolytkondensatoren, bei denen es vor allem auf einen möglichst großen Kapazitätswert ankommt, kommen auch Toleranzen wie z. B. +100/-20% vor.
Merke: Die Toleranz (mit Ausnahme von 20%) wird im allgemeinen in Klarschrift auf den Kondensatorkörper aufgedruckt, bei sehr kleinen Abmessungen kommt es auch zur Verschlüsselung oder Codierung.
Nach längerer Lagerung oder längerem Gebrauch kann die Toleranz nach oben abweichen; jedoch darf sie nach Norm niemals den doppelten Wert der Auslieferung überschreiten.
Üblich sind bei Wickelkondensatoren folgende Auslieferungstoleranzen:
±1%; ±2,5%; ±5%; ±10%; ±20%.
Bei Elektrolytkondensatoren, bei denen es vor allem auf einen möglichst großen Kapazitätswert ankommt, kommen auch Toleranzen wie z. B. +100/-20% vor.
Merke: Die Toleranz (mit Ausnahme von 20%) wird im allgemeinen in Klarschrift auf den Kondensatorkörper aufgedruckt, bei sehr kleinen Abmessungen kommt es auch zur Verschlüsselung oder Codierung.
Nennspannung / Spannungsderating
Jeder Kondensator ist für eine bestimmte Nennspannung ausgelegt, die er im Dauerbetrieb ohne Schaden aushalten muss.
Sie gilt allerdings nur für Umgebungstemperaturen < +85°C, bei höheren Temperaturen wird die max. zulässige Spannung oder "Dauergrenzspannung" durch Spannungsderating herabgesetzt.
Die Ursache hierfür sind winzige Schwachstellen im Dielektrikum, die bei erhöhter Temperatur stärker beansprucht werden und dann durchschlagen können.
Bei der Nennspannung unterscheidet man zwischen Gleich- und Wechselspannungsangaben. Im allgemeinen sind diese Angaben in Klarschrift aufgedruckt, bei sehr kleinen Kondensatorabmessungen kann ebenso wie bei der Toleranzangabe eine Verschlüsselung oder Codierung notwendig werden.
Bei allen thermoplastischen Kunststofffoliendielektrika sinkt die Spannungsfestigkeit mit wachsender Temperatur.
Das Spannungsderating gibt an, um wieviel Prozent sich die zulässige Spannung gegenüber der Nennspannung bei Gleichspannungsbetrieb ab +85°C, bei Wechselspannungsbetrieb ab +75°C bei 1K Temperaturzuwachs vermindert
Sie gilt allerdings nur für Umgebungstemperaturen < +85°C, bei höheren Temperaturen wird die max. zulässige Spannung oder "Dauergrenzspannung" durch Spannungsderating herabgesetzt.
Die Ursache hierfür sind winzige Schwachstellen im Dielektrikum, die bei erhöhter Temperatur stärker beansprucht werden und dann durchschlagen können.
Bei der Nennspannung unterscheidet man zwischen Gleich- und Wechselspannungsangaben. Im allgemeinen sind diese Angaben in Klarschrift aufgedruckt, bei sehr kleinen Kondensatorabmessungen kann ebenso wie bei der Toleranzangabe eine Verschlüsselung oder Codierung notwendig werden.
Spannungsderating:
Bei allen thermoplastischen Kunststofffoliendielektrika sinkt die Spannungsfestigkeit mit wachsender Temperatur.
Das Spannungsderating gibt an, um wieviel Prozent sich die zulässige Spannung gegenüber der Nennspannung bei Gleichspannungsbetrieb ab +85°C, bei Wechselspannungsbetrieb ab +75°C bei 1K Temperaturzuwachs vermindert
Isolationswiderstand
Papier- und Kunststofffolienkondensatoren haben im Anlieferungszustand üblicherweise Isolationswiderstandswerte im Bereich zwischen 6000 und 12000 MΩ.
Neben der Angabe des Isolationswiderstandes in Ohm - sie ist nicht ganz eindeutig, da sich der Isolationswiderstand nach Anlegen der Spannung noch einige Zeit verändert - wird auch die Selbstentladezeitkonstante Τ = Ris · C als Maß für die Isolationsgüte verwendet.
Die Zeitkonstante gibt die Zeit in sec an, innerhalb der die Spannung zwischen den Anschlußdrähten eines aufgeladenen Kondensators durch Selbstentladung um 37% abgesunken ist.
Bei Kapazitätswerten im µF Bereich liegt die Zeitkonstante bei Anlieferung im allgemeinen zwischen 2000 und 4000 sec.
Feuchtigkeit, die in den Kondensatorwickel eindringt, setzt den Isolationswiderstand herab. Je nach Feuchtigkeitsbeanspruchung muß daher eine entsprechend dichte Umhüllung vorgesehen werden.
Guter Isolationswiderstand ist notwendig bei Kondensatoren, die zur Abriegelung von Gleichspannungen dienen und bei Speicherkondensatoren, die einen bestimmten Spannungswert längere Zeit unverändert beibehalten müssen.
Neben der Angabe des Isolationswiderstandes in Ohm - sie ist nicht ganz eindeutig, da sich der Isolationswiderstand nach Anlegen der Spannung noch einige Zeit verändert - wird auch die Selbstentladezeitkonstante Τ = Ris · C als Maß für die Isolationsgüte verwendet.
Die Zeitkonstante gibt die Zeit in sec an, innerhalb der die Spannung zwischen den Anschlußdrähten eines aufgeladenen Kondensators durch Selbstentladung um 37% abgesunken ist.
Bei Kapazitätswerten im µF Bereich liegt die Zeitkonstante bei Anlieferung im allgemeinen zwischen 2000 und 4000 sec.
Feuchtigkeit, die in den Kondensatorwickel eindringt, setzt den Isolationswiderstand herab. Je nach Feuchtigkeitsbeanspruchung muß daher eine entsprechend dichte Umhüllung vorgesehen werden.
Guter Isolationswiderstand ist notwendig bei Kondensatoren, die zur Abriegelung von Gleichspannungen dienen und bei Speicherkondensatoren, die einen bestimmten Spannungswert längere Zeit unverändert beibehalten müssen.
Verlustfaktor und ESR
Der Verlustfaktor tanδ ist der Quotient aus Wirk- und Blindanteil des Scheinwiderstandes.
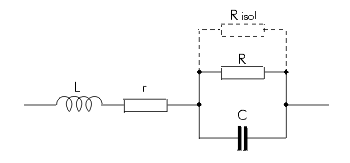
Die Verluste entstehen hauptsächlich im Dielektrikum, dargestellt durch R im Ersatzschaltbild.
Parallel zu R liegt der Isolationswiderstand Ris, der allerdings nur bei sehr niedrigen Frequenzen tanδ beeinflußt.
Weitere Verluste sind bedingt durch die endliche Leitfähigkeit der Kondensatorbeläge und den Übergangswiderstand zwischen Belägen und Anschlußdrähten, dargestellt im Ersatzschaltbild durch den Reihenwiderstand r. L stellt die verbleibende Eigeninduktivität dar.
Der Verlustfaktor ist z. B. bei Wechselstromkondensatoren, die mit starken Strömen belastet werden, von Bedeutung: Ein zu großer tanδ kann durch die aufgenommene Wirkleistung zu übermäßiger Erwärmung und damit zu verkürzter Lebensdauer führen.
ESR-Werte werden nicht in den jeweiligen Datenblättern der einzelnen Reihen genannt. Werte für bestimmte Kapazitäten können nach folgender Formel berechnet werden:
ESR = tanδ · (2 · π · f · C)-1
tanδ: siehe Datenblatt der jeweiligen WIMA-Reihe.
f: Frequenz des Wechselspannungsanteils in der Applikation
Parallel zu R liegt der Isolationswiderstand Ris, der allerdings nur bei sehr niedrigen Frequenzen tanδ beeinflußt.
Weitere Verluste sind bedingt durch die endliche Leitfähigkeit der Kondensatorbeläge und den Übergangswiderstand zwischen Belägen und Anschlußdrähten, dargestellt im Ersatzschaltbild durch den Reihenwiderstand r. L stellt die verbleibende Eigeninduktivität dar.

Der Verlustfaktor ist z. B. bei Wechselstromkondensatoren, die mit starken Strömen belastet werden, von Bedeutung: Ein zu großer tanδ kann durch die aufgenommene Wirkleistung zu übermäßiger Erwärmung und damit zu verkürzter Lebensdauer führen.
ESR (Equivalent Series Resistance)
ESR-Werte werden nicht in den jeweiligen Datenblättern der einzelnen Reihen genannt. Werte für bestimmte Kapazitäten können nach folgender Formel berechnet werden:
ESR = tanδ · (2 · π · f · C)-1
tanδ: siehe Datenblatt der jeweiligen WIMA-Reihe.
f: Frequenz des Wechselspannungsanteils in der Applikation
Induktivität und Eigenresonanz
Je nach Aufbau erzeugt ein Wechselstrom im Kondensatorwickel ein mehr oder weniger ausgeprägtes Magnetfeld, das sich als Induktivität L messen läßt (s.a. Ersatzschaltbild).

Die Eigeninduktivität L moderner Kondensatoren liegt - durch konstruktive Maßnahmen (z.B. Stirnkontaktierung) reduziert - bei ca. 10 nH. Sie ist somit nicht größer als die Induktivität eines Drahtes, der ebenso lang wie die Bandlänge des Kondensatorwickels ist.
L und C bilden einen Serienschwingkreis; bei der Frequenz
ist der Kondensator in Eigenresonanz, er hat dann den niedrigsten Scheinwiderstand, der nur noch aus r besteht (ESR)

Die Eigeninduktivität L moderner Kondensatoren liegt - durch konstruktive Maßnahmen (z.B. Stirnkontaktierung) reduziert - bei ca. 10 nH. Sie ist somit nicht größer als die Induktivität eines Drahtes, der ebenso lang wie die Bandlänge des Kondensatorwickels ist.
L und C bilden einen Serienschwingkreis; bei der Frequenz
| f0 = 12π · √L · C |
ist der Kondensator in Eigenresonanz, er hat dann den niedrigsten Scheinwiderstand, der nur noch aus r besteht (ESR)
Temperaturkoeffizient (TKc)
Der Temperaturkoeffizient α gibt an, um welchen Bruchteil sich der bei +20°C gemessene Kapazitätswert ändert, wenn die Umgebungstemperatur um 1 Grad C steigt.
C20 = Kapazität bei+20°C
CT = Kapazität bei T°C
α kann positiv oder negativ sein. Bei guten Kondensatoren liegt der TKc in der Größenordnung von wenigen 10-5/°C.
TKc 10-5/°C = 10 · 10-6/°C = 10 ppm/°C
| CT = C20 · [1 + α · (T - 20° C)] |
C20 = Kapazität bei+20°C
CT = Kapazität bei T°C
α kann positiv oder negativ sein. Bei guten Kondensatoren liegt der TKc in der Größenordnung von wenigen 10-5/°C.
TKc 10-5/°C = 10 · 10-6/°C = 10 ppm/°C
Impulsbelastung
Bei metallisierten Kondensatoren müssen dem Anwender infolge der begrenzten Strombelastbarkeit von Belägen und Kontaktierung Richtlinien für eine max. mögliche Impulsbelastung gegeben werden.
Diese Richtlinien werden durch sogenannte Impulsprüfungen ermittelt, in denen die im Anwendungsfall möglicherweise auftretenden Belastungen simuliert werden.
In einer Prüfschaltung entsprechend DIN-IEC 60384 Teil 1 wird der Prüfling aufgeladen und anschließend stoßartig entladen: Die Prüfspannung entspricht der Nenngleichspannung, die Prüfung erfolgt mit 10000 Impulsen, die Folgefrequenz beträgt 1 Hz.
Die Angaben der Impulsbelastbarkeit erfolgen als Flankensteilheit in V/µsec. Die Angaben für einzelne Kondensatorenreihen sind z.B. aus den CECC Bauartspezifikationen abgeleitet. Die Nenn- bzw. Betriebs-Flankensteilheit wird mit 1/10 der Prüf-Flankensteilheit vorgeschrieben.
Die Angabe der Flankensteilheit F in V/µsec ist indirekt die Angabe für die maximale Strombelastbarkeit.
C in µF
I in A
Die Angaben für die Flankensteilheit beziehen sich auf den vollen Nennspannungshub, so daß bei kleineren Betriebsspannungen auch die zulässigen Flankensteilheiten zunehmen können.
Diese Richtlinien werden durch sogenannte Impulsprüfungen ermittelt, in denen die im Anwendungsfall möglicherweise auftretenden Belastungen simuliert werden.
In einer Prüfschaltung entsprechend DIN-IEC 60384 Teil 1 wird der Prüfling aufgeladen und anschließend stoßartig entladen: Die Prüfspannung entspricht der Nenngleichspannung, die Prüfung erfolgt mit 10000 Impulsen, die Folgefrequenz beträgt 1 Hz.
Die Angaben der Impulsbelastbarkeit erfolgen als Flankensteilheit in V/µsec. Die Angaben für einzelne Kondensatorenreihen sind z.B. aus den CECC Bauartspezifikationen abgeleitet. Die Nenn- bzw. Betriebs-Flankensteilheit wird mit 1/10 der Prüf-Flankensteilheit vorgeschrieben.
Die Angabe der Flankensteilheit F in V/µsec ist indirekt die Angabe für die maximale Strombelastbarkeit.
| I = F · C · 1,6 |
C in µF
I in A
Die Angaben für die Flankensteilheit beziehen sich auf den vollen Nennspannungshub, so daß bei kleineren Betriebsspannungen auch die zulässigen Flankensteilheiten zunehmen können.
Langzeitstabilität / Zeitliche Inkonstanz
Umwelteinflüsse wie Wärme, hohe Feuchtigkeit und starke mechanische Erschütterung können über längere Zeit durch Alterung zu einer bleibenden Veränderung des Kapazitätswertes führen.
Durch die Angabe der zeitlichen Inkonstanz wird festgelegt, bis zu welchem Maß sich die Kapazität eines Kondensators unter der Einwirkung von Umwelteinflüssen max. verändern darf.
In der Regel wird die zeitliche Inkonstanz in % angegeben. Als Zeitspanne geben die einschlägigen Normen zwei Jahre vor, wobei regelmäßig auf eine Temperatur von +40°C bezogen wird. Änderungen nach zwei Jahren fallen kaum ins Gewicht.
Typische Werte sind z.B. bei KT- /MKT-Kondensatoren ±3%, bei KP- /MKP-Kondensatoren je nach Ausführung ±0.5 bzw. ±1%.
Durch die Angabe der zeitlichen Inkonstanz wird festgelegt, bis zu welchem Maß sich die Kapazität eines Kondensators unter der Einwirkung von Umwelteinflüssen max. verändern darf.
In der Regel wird die zeitliche Inkonstanz in % angegeben. Als Zeitspanne geben die einschlägigen Normen zwei Jahre vor, wobei regelmäßig auf eine Temperatur von +40°C bezogen wird. Änderungen nach zwei Jahren fallen kaum ins Gewicht.
Typische Werte sind z.B. bei KT- /MKT-Kondensatoren ±3%, bei KP- /MKP-Kondensatoren je nach Ausführung ±0.5 bzw. ±1%.
Dielektrische Absorption
Dielektrische Absorption ist der Effekt, daß ein längere Zeit aufgeladener Kondensator nach seiner vollständigen Entladung innerhalb von Sekunden bis Minuten wieder eine kleine Spannung an seinen Anschlußdrähten aufweist.
Besonders nachteilig wirkt sich diese Erscheinung für Kondensatoren aus, in denen zu Meßzwecken Ladungen gespeichert werden sollen. Die Nachladung rührt von Polarisierungsvorgängen im Isolierstoff her und ist weitgehend unabhängig von der Kapazität des Kondensators und der Dielektrikumsdicke.
Beispielhaft wird die Messung der dielektrischen Absorption auf der Grundlage des Standards MIL-C-19978 D beschrieben.
Schaltbild:
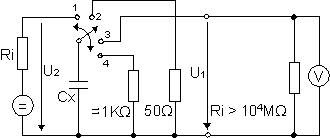
Der Kondensator Cx wird 15 Minuten an einer Bezugsgleichspannung aufgeladen, z.B. auf die Nenn-Gleichspannung des Kondensators. Dabei darf der Anfangsstromstoß 50 mA nicht überschreiten. Am Ende der Ladezeit wird der Kondensator von der Ladungsquelle getrennt und über einen 50 Ω - Widerstand entladen. Der Entladewiderstand wird nach 10 sec vom Kondensator entfernt. Die "wiedergewonnene Spannung" wird nach einer Dauer von 15 min. mit einem hochohmigen (Ri > 10000 MΩ) Millivoltmeter gemessen.
Die dielektrische Absorption (DA) kann nach der folgenden Formel berechnet werden:
DA = U1 / U2 · 100%
DA = dielektrische Absorption
U1 = wiedergewonnene Spannung
U2 = Ladespannung
Typische Werte einiger Dielektrika in % bei T = +23°C:
Besonders nachteilig wirkt sich diese Erscheinung für Kondensatoren aus, in denen zu Meßzwecken Ladungen gespeichert werden sollen. Die Nachladung rührt von Polarisierungsvorgängen im Isolierstoff her und ist weitgehend unabhängig von der Kapazität des Kondensators und der Dielektrikumsdicke.
Messung der dielektrischen Absorption
Beispielhaft wird die Messung der dielektrischen Absorption auf der Grundlage des Standards MIL-C-19978 D beschrieben.
Schaltbild:

Der Kondensator Cx wird 15 Minuten an einer Bezugsgleichspannung aufgeladen, z.B. auf die Nenn-Gleichspannung des Kondensators. Dabei darf der Anfangsstromstoß 50 mA nicht überschreiten. Am Ende der Ladezeit wird der Kondensator von der Ladungsquelle getrennt und über einen 50 Ω - Widerstand entladen. Der Entladewiderstand wird nach 10 sec vom Kondensator entfernt. Die "wiedergewonnene Spannung" wird nach einer Dauer von 15 min. mit einem hochohmigen (Ri > 10000 MΩ) Millivoltmeter gemessen.
Die dielektrische Absorption (DA) kann nach der folgenden Formel berechnet werden:
DA = U1 / U2 · 100%
DA = dielektrische Absorption
U1 = wiedergewonnene Spannung
U2 = Ladespannung
Typische Werte einiger Dielektrika in % bei T = +23°C:
| - Polypropylen - Polyester - Mischdielektrikum - Keramik (X7R) - Keramik (Z5U) |
0,05 ... 0,10 0,20 ... 0,25 0,12 ... 0,18 0,60 ... 1,00 2,00 ... 2,50 |
Zuverlässigkeit
Für den Kunststofffolienkondensator gilt für die Ausfallrate in fit (10-9/h) die Formeldarstellung
λo = Erwartungswert
πT = Temperaturfaktor
πU = Spannungsfaktor
Der Erwartungswert wird für jedes Bauelement aufgrund von Langzeitversuchen und Felderfahrungen ermittelt. Langzeitversuche beziehen sich auf eine Mindestprüfdauer von t > 10000 h.
Erfolgt eine solche Prüfung z.B. bei 85°C, dann entspricht das in einem Gerät mit T < 40°C Umgebungstemperatur einer Betriebszeit von ca. 150000 - 200000 h; ein Wert, der sicherlich den realen Einsatzbedingungen nahekommt. Wegen der auch in der Literatur beschriebenen Unsicherheiten über die Genauigkeit dieser Hochrechnungen wird der Wert mit einer Vertrauensgrenze von 60% angegeben. Die Werte decken sich jedoch nach unserer Erfahrung weitgehend mit den Feldergebnissen.
Korrekturfaktoren ergeben sich anwendungsspezifisch aus der Stressbelastung (Temperatur und/oder Spannung) nach folgenden Tabellen:
λo = 2 fit
πT = 1
πU = 5
λ = 2 · 5 · 1 = 10 fit
Erwartungswerte für andere Kondensatorentypen entnehmen Sie bitte den entsprechenden Datenblättern.
| λ = λo · πT · πU |
λo = Erwartungswert
πT = Temperaturfaktor
πU = Spannungsfaktor
Der Erwartungswert wird für jedes Bauelement aufgrund von Langzeitversuchen und Felderfahrungen ermittelt. Langzeitversuche beziehen sich auf eine Mindestprüfdauer von t > 10000 h.
Erfolgt eine solche Prüfung z.B. bei 85°C, dann entspricht das in einem Gerät mit T < 40°C Umgebungstemperatur einer Betriebszeit von ca. 150000 - 200000 h; ein Wert, der sicherlich den realen Einsatzbedingungen nahekommt. Wegen der auch in der Literatur beschriebenen Unsicherheiten über die Genauigkeit dieser Hochrechnungen wird der Wert mit einer Vertrauensgrenze von 60% angegeben. Die Werte decken sich jedoch nach unserer Erfahrung weitgehend mit den Feldergebnissen.
Korrekturfaktoren ergeben sich anwendungsspezifisch aus der Stressbelastung (Temperatur und/oder Spannung) nach folgenden Tabellen:
Temperaturfaktor πT
| T (°C) | 40 | 50 | 70 | 80 | 100 |
| πT | 1 | 2 | 5 | 10 | 15 |
Spannungsfaktor πU
| U/UR | 0,1 | 0,25 | 0,5 | 0,75 | 1,0 |
| πU | 0,2 | 0,3 | 1 | 2 | 5 |
Die besten Werte erreichen heute z.B. metallisierte Kunststofffolienkondensatoren mit Polyester-Folie.
Der Erwartungswert liegt hier bei 2 fit. Hieraus ergibt sich dann eine Ausfallrate von 10 fit.
Beispiel: WIMA MKS 2 / 0,1 µF / 63 V-
λo = 2 fit
πT = 1
πU = 5
λ = 2 · 5 · 1 = 10 fit
Erwartungswerte für andere Kondensatorentypen entnehmen Sie bitte den entsprechenden Datenblättern.
Warnhinweise / Technische Beratung
Wechselspannungsbelastung am Netz
Gleichspannungskondensatoren, unabhängig von ihrer Wechselspannungsangabe, dürfen mit Rücksicht auf Störimpulse nicht am Netz betrieben werden. Hierzu sind ausschließlich approbierte Funkentstör-Kondensatoren zu verwenden.
Wärmebelastung in der Applikation
Wird ein Kunststofffolien-Kondensator durch unsachgemäßen Einsatz unter Wechselspannung überbelastet, kann es zu einem unzulässig hohen Temperaturanstieg im Bauelement kommen. Dies kann zu einer Schädigung der Dielektrikumsfolie und in der Folge zu einem Kurzschluss bzw. zu Rauchentwicklung oder gar Brand des Kondensators führen. Derselbe Fall kann eintreten, wenn der Kondensator durch eine fremde Wärmequelle überhitzt wird.
Schock- und/oder Vibrationsüberbelastung bei größeren Bauformen
Treten in einer Applikation erhöhte Schock- bzw. Vibrationsbelastungen auf, wird empfohlen, voluminöse Kondensatoren, z.B. ab Rastermaß 22,5 mm, in geeigneter Weise zu fixieren, um Anschlussdrähte oder Lötverbindungen zu entlasten.
Verarbeitung
Bei der Verarbeitung von Kunststofffolien-Kondensatoren sind unbedingt die Applikationsempfehlungen bezüglich Lötverfahren bzw. Reinigungs- und Trocknungsprozesse zu beachten.
Allgemeine Hinweise
Alle Katalogdaten, Werteübersichten und Applikationshinweise entsprechen dem aktuellen technischen Stand und wurden so sorgfältig wie möglich ausgearbeitet. Sie sind als grundsätzliche Information zu verstehen. Abweichungen und Konstruktionsänderungen behalten wir uns vor. Von den Katalogangaben abweichende, kundenspezifische Sonderanfertigungen entbinden, unabhängig von zugrundeliegenden Werknormen, Spezifikationen o.ä., den Anwender nicht von seiner Sorgfaltspflicht hinsichtlich der Wareneingangs- und Fertigungskontrollen. Bei Bezug von Bauteilen über Zweit- oder Drittanbieter empfehlen wir unbedingt den Abgleich technischer Daten mit den Herstellerangaben. Im Zweifelsfall sollte immer unsere technische Beratung in Anspruch genommen werden, da wir für Schäden die durch unsachgemäße Verarbeitung oder Anwendung unserer Kondensatoren entstehen, keine Verantwortung übernehmen können.
Gleichspannungskondensatoren, unabhängig von ihrer Wechselspannungsangabe, dürfen mit Rücksicht auf Störimpulse nicht am Netz betrieben werden. Hierzu sind ausschließlich approbierte Funkentstör-Kondensatoren zu verwenden.
Wärmebelastung in der Applikation
Wird ein Kunststofffolien-Kondensator durch unsachgemäßen Einsatz unter Wechselspannung überbelastet, kann es zu einem unzulässig hohen Temperaturanstieg im Bauelement kommen. Dies kann zu einer Schädigung der Dielektrikumsfolie und in der Folge zu einem Kurzschluss bzw. zu Rauchentwicklung oder gar Brand des Kondensators führen. Derselbe Fall kann eintreten, wenn der Kondensator durch eine fremde Wärmequelle überhitzt wird.
Schock- und/oder Vibrationsüberbelastung bei größeren Bauformen
Treten in einer Applikation erhöhte Schock- bzw. Vibrationsbelastungen auf, wird empfohlen, voluminöse Kondensatoren, z.B. ab Rastermaß 22,5 mm, in geeigneter Weise zu fixieren, um Anschlussdrähte oder Lötverbindungen zu entlasten.
Verarbeitung
Bei der Verarbeitung von Kunststofffolien-Kondensatoren sind unbedingt die Applikationsempfehlungen bezüglich Lötverfahren bzw. Reinigungs- und Trocknungsprozesse zu beachten.
Allgemeine Hinweise
Alle Katalogdaten, Werteübersichten und Applikationshinweise entsprechen dem aktuellen technischen Stand und wurden so sorgfältig wie möglich ausgearbeitet. Sie sind als grundsätzliche Information zu verstehen. Abweichungen und Konstruktionsänderungen behalten wir uns vor. Von den Katalogangaben abweichende, kundenspezifische Sonderanfertigungen entbinden, unabhängig von zugrundeliegenden Werknormen, Spezifikationen o.ä., den Anwender nicht von seiner Sorgfaltspflicht hinsichtlich der Wareneingangs- und Fertigungskontrollen. Bei Bezug von Bauteilen über Zweit- oder Drittanbieter empfehlen wir unbedingt den Abgleich technischer Daten mit den Herstellerangaben. Im Zweifelsfall sollte immer unsere technische Beratung in Anspruch genommen werden, da wir für Schäden die durch unsachgemäße Verarbeitung oder Anwendung unserer Kondensatoren entstehen, keine Verantwortung übernehmen können.
